设u=2xy-z^2,则u在点(2,-1,1)处的方向导数的最大值为( )。
A. 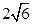 B. 4
C. (-2,-4,-2)
D. 6
B. 4
C. (-2,-4,-2)
D. 6
查看答案
热门试题
设函数u=u(x,y)满足∂2u/∂x2-∂2u/∂y2=0及条件u(x,2x)=x,ux′(x,2x)=x2,u有二阶连续偏导数,则uxx″(x,2x)=( )。
设函数u=u(x,y),x=x(ξ,η),y=y(ξ,η)都有二阶连续偏导数,且∂x/∂ξ=∂y/∂η,∂x/∂η=-∂y/∂ξ。 证明:∂2u/∂ξ2+∂2u/∂η2=[(∂x/∂ξ)2+(∂y/∂ξ)2]·(∂2u/∂x2+∂2u/∂y2)。
函数在某点的方向导数存在, 则函数在此点的偏导数存在。(? ? ??)
函数在某点的方向导数存在, 则函数在此点的偏导数存在()
已知一交流电$u = 220\sqrt{2}\sin(100\pi t + 45^{\circ})$,则其最大值为( )
函数f’(x,y,z)=x^2y+z^2在点(1,2,0)处沿向量n=(1,2,2)的方向导数为
设二元函数F的两个偏导数F1′、F2′不同时为零,另一个二元函数u(x,y)满足F(∂u/∂x,∂u/∂y)=0(其中u(x,y)有二阶连续偏导数),证明:(∂2u/∂x2)·(∂2u/∂y2)=(∂2u/∂x∂y)2。
(Ⅰ)设函数u(x),ν(x)可导,利用导数定义证明[u(x)ν(x)]’=u’(x)ν(x)+u(x)ν’(x); (Ⅱ)设函数u1(x),u2(x),…,un(x)可导,f(x)=u1(x)u2(x)…un(x),写出f(x)的求导公式.
当成数方差取得最大值时,p 趋近于 。( )
有两个频率和初相位不同的正弦交流电压u1和u2,,若它们的有效值相同,则最大值也相同.()
有两个频率和初相位不同的正弦交流电压u1和u2,若他们的有效值相同,则最大值也相同()
有两个频率和初相位不同的正弦交流电压u1和u2,,若它们的有效值相同,则最大值也相同()
偏导数、方向导数都是研究某点沿给定方向的()
(Ⅰ)设函数u(x),v(x)可导,利用导数定义证明[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x);(Ⅱ)设函数u1(x),u2(x),…,un(x)可导,f(x)=u1(x)u2(x)…un(x),写出f(x)的求导公式。
有两个频率和初相角都不同的正弦交流电压u1和u2,若它们的有效值相同,则最大值也相同()
设U1=Um1sin(wt+?1),U2=U㎡sin(wt+?2),如果Δ?=?1-?2=180°,则称U1和U2( )。
设z=f(u),而u=u(x,y)满足u=y+xφ(u)。若f和φ有连续导数,u存在偏导数,且xφ′(u)≠1,证明:∂z/∂x=φ(u)∂z/∂y。
设X~U(2,4),则E(2X+2)=
梯度是方向导数的最值()。
单向半波可控整流电路,若变压器次级电压为u2,则输出平均电压的最大值为()



