若α2+b2=c2,且a,b,c均为正整数,则a,b,c三个数为勾股数,从3,4,12,13 中任取两个数,其中能和5组成勾股数的概率是()
A. 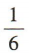 B.
B. 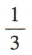 C.
C. 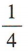 D.
D. 
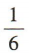
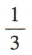
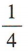

查看答案
热门试题
设两两相互独立的三个事件A、B、C满足条件ABC=∅,P(A)=P(B)=P(C)<1/2,且已知P(A∪B∪C)=9/16,则P(A)=____。
在△ABC中,∠A=60°,∠C=2∠B,则∠C=()
已知a、b、c、d都是正整数,且a>b>c>d,a+b+c+d=2004,2a-2b+2c-2d=2004,则a+d的最小值是( )。
在△ABC中,角A,B,C的对边分别是a,b,c,若c2=a2+ab+b2,则C=()
在△ABC中,a=2,b=3,c=135°,则△ABC的面积等于().
在△ABC中,内角A,B,C的对边分别为a,b,c,且a=3,b=2,A=60°.
(1)求sinB;
(2)求△ABC的面积
三个数字ABC,其中A>B、B>C,可知A>C,这时运用的思维是()
自然数、正整数和整数这三个数概念中,()的范围最大。
设△ABC 的三条边分别是 a,b,c,且 a2+b2=c2。证明:△ABC 是直角三角形。(这是勾股定理的逆命题)
已知三角形ABC的三条边分别为a,b,c.则三角形ABC是等腰直角三角形(1)(a-b)(c2-a2-b2)=0(2)c=√2b
在△ABC中,内角A,B,C的对边分别为a,b,c,若sinA:sinB=2:3,则a:b=()
已知△ABC的内角A,B,C的对边分别为a,b,c,且a²=b²-c²-√2ac,则角B=()
在△ABC中,A,B,C所对的边分别为a,b,c,若a=2,b=1,c=60°,则c=()。
如果A、B、C、D分别代表1-9中一个数字,且2×AA+BB+3=DCD=DD×DD,则ABC×D=( )
在△ABC中,内角A,B,C所对的边分别为a,b,c,且B=60°,a=2,c=1,则b=()
已知△ABC中,∠A,∠B,∠C所对边为a,b,c,C=30°,a=c=2,则b=____.
已知△ABC内角A,B,C所对的边分别为a,b,c,若a=3,b=2,A=60°,则cos B=().
每一个确定的正整数a,都有一个确定的后继数a’,a’也是正整数(一个数的后继数就是紧接在这个数后面的数,例如,1的后继数是2,2的后继数是3等等).那么1()任何正整数的后继数
每一个确定的正整数a,都有一个确定的后继数a’,a’也是正整数(一个数的后继数就是紧接在这个数后面的数,例如,1的后继数是2,2的后继数是3等等).那么1()任何正整数的后继数
在△ABC中,已知2B=A+C,b2=ac,则B-A=()。



