设函数f(x)在x=0处可导,且f(0)=0,f′(0)≠0,则下列极限存在且为零的是()
A.  B.
B. 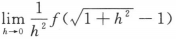 C.
C. 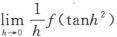 D.
D. 

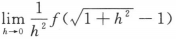
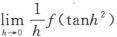

查看答案
热门试题
设可导函数f(x)满足xf′(x)-f(x)>0,则()。
设y=f(x)在点x=0处可导,且x=0为f(x)的极值点,则f’(0)=()。
设函数f(x)在(0,1)上可导且在[0,1]上连续,且f'(x)>0,f(0)<0,f(1)>0,则f(x)在(0,1)内()。
设函数f(x)在x=x0的某邻域内连续,在x=x0处可导,则函数f(x)|f(x)|在x=x0处()
设y=f(x)二阶可导,且,f′(1)=0,f″(1)>0,则必有().
设f(x)是R上的可导函数,且f(x)>0。若f?(x)-3x2f(x)=0,且f(0)=1,求f(x)。
设 f(x)是 R 上的可导函数,且 f(x)>0。若 f"(x)-3x---2f(x)=0,且 f(0)=1,求 f(x)。
设f(x)可导,F(x)=f(x)[1-|ln(1+x)|],则f(0)=0是F(x)在x=0处可导的( )。
设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=____。
设f(x)是可导函数,且f′(x)=sin(x+1),f(0)=4,x=g(y)是y=f(x)的反函数,则g′(4)=().
设函数f(x)在(0,1)内可导,f"(x)>0,则f(x)在(0,1)内( )
设函数f(x)在(0,1)内可导,f'(x)>0,则f(x)在(0,1)内()。
设函数f(x)在x=0可导且f(0)=1,又设f(x)满足函数方程f(x+1)=2f(x),求f′(n),其中n是整数。
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有( )。
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有()
设函数f(x)在[0,1]上连续,在(0,1)内二阶可导,且f′(x)<0,f"(x)<0,则下列结论成立的是()
设f(x)是R上的可导函数,且f(x)>0。(1)求lnf(x)的导函数;
(2)已知f,(x)-3x2f(x)=0,且f(0)=1,求f(x)。 求证:设函数f(x),g(x)在点x=a可导,f(a)=g(a)=0且存在δ>0,使得当0<|x-a|<δ时,有|f(x)|≥|g(x)|,则|f′(a)|≥|g′(a)|。 设函数f(x)在[a,b]连续,在(a,b)可导,f'(x)>0,若f(a)·f(b) 设函数f(x)连续,且f′(0)>0,则存在δ>0,使得( )。
(2)已知f,(x)-3x2f(x)=0,且f(0)=1,求f(x)。 求证:设函数f(x),g(x)在点x=a可导,f(a)=g(a)=0且存在δ>0,使得当0<|x-a|<δ时,有|f(x)|≥|g(x)|,则|f′(a)|≥|g′(a)|。 设函数f(x)在[a,b]连续,在(a,b)可导,f'(x)>0,若f(a)·f(b) 设函数f(x)连续,且f′(0)>0,则存在δ>0,使得( )。



