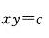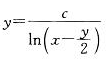微分方程ydx+(x-y)dy=0的通解是:(c为任意常数)   

微分方程y′′-4y=4的通解是(C1，C2为任意常数）： 在下列微分方程中，以函数y＝C1e^－x＋C2e^4x（C1，C2为任意常数）为通解的微分方程是（　　）。 已知微分方程y"+p（x）y = q（x）[q（x）≠0]有两个不同的特解y1（x）， y2（x），C为任意常数，则该微分方程的通解是： 已知微分方程y"+p(x)y=q(x)[q(x)≠0]有两个不同的特解：y1(x)，y2(x)，则该微分方程的通解是:（c为任意常数） （2012）已知微分方程y′+p+（x）y=q（x）［q（x）≠0］有两个不同的特解y1（x），y2（x），则该微分方程的通解是：（c为任意常数）（） 微分方程y""+y=0的通解是 . 微分方程y''+y=0的通解是（）。   微分方程y’=0的通解为（）。   函数：（：为任意常数）是微分方程y”-y’-2y=0的（） 微分方程y”+y’=0的通解为（）。   微分方程y′-y=0的通解为（） 微分方程y′-y=0的通解为()． 微分方程xy"-ylny=0的通解为()。 设C是任意常数,则下列以y=Ce^x为解的二阶微分方程是()   微分方程的通解包含了所有的解 若A、B为非零常数，C1、C2为任意常数，则微分方程y″+k2y=cosx的通解应具有形式( )。 设非齐次线性微分方程y′+P（x）y=Q（x）有两个不同的解y1（x），y2（x），C为任意常数，则该方程通解是（） 微分方程y″+2y=0的通解是( )。 微分方程y""+2y=0的通解是： 微分方程y”+9y=0的通解是().