注册 下载APP 帮助中心
当前位置：首页 > 考试 > 学历类 > 高职单招 > 数学(中职) >
2025年高职单招每日一练《数学(中职)》5月14日

2025年高职单招每日一练《数学(中职)》5月14日

考试总分：8分

考试类型：模拟试题

作答时间：60分钟

已答人数：228

试卷答案：有

试卷介绍：2025年高职单招每日一练《数学(中职)》5月14日专为备考2025年数学(中职)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

开始答题

试卷预览

单选题 主观题 填空题 简答题
  • 1. 函数f(x)=log2(x+1)的定义域为()  

    A(-∞,-1)

    B[-1,+∞)

    C(-1,+∞)

    D(1,+∞)

  • 2. 从3名男志愿者和2名女志愿者中选2名去支援“冰壶”比赛的相关工作,若冰壶项目需要1男1女两名志愿者,则不同的支援方法的种数是()

    A2

    B4

    C6

    D12

  • 3. 函数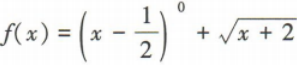的定义域为()

    A

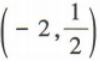
    B[-2,+∞)

    C

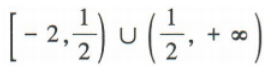
    D

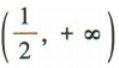
  • 1. 已知
  • 1. 在二项式(x-1)6的展开式中,系数最小的项是第()项.  
  • 2. 设等比数列{an}的前n项和为Sn,已知a1=3,S6=3S3,则a7=（）
  • 3. 已知点P在圆x2+(y-1)2=9上,若点P到直线y=x+1的距离为3,则满足条件的点P的个数为（）  
  • 1. 设数列{an}的前n项和为n(n+1)，数列的{bn}第n项是数列{an}的第2n项，即bn=a2n. （1）求数列{an}的通项公式. （2）求数列{bn}的前n项和. （3）证明：对任意的正整数n和k(k＜n)，都有.
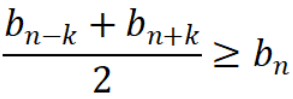
相关试卷
相关题库